Overview of Support Vector Machines
Chew, Hong Gunn
19 November, 1998
Vapnik first introduced Support Vector Machines (SVMs) in 1979. However, it has only gained attention in the last few years. SVM has been shown to be suitable for pattern recognition.

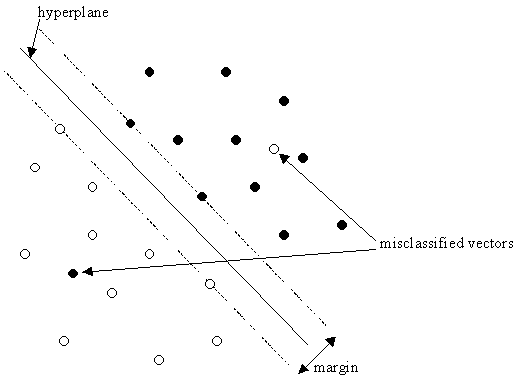
Figure 1
The training of a classification SVM involves the fitting of a hyperplane such that the largest margin is formed between 2 classes of vectors while minimising the effects of classification errors (figure 1). This is solved by formulating it as a convex quadratic programming problem. Without going into the details, this gives the Lagrangian:
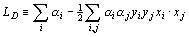 |
(1) |
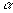

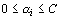
The parameter C is to be chosen by the user, where a larger
C will assign a higher penalty to classification errors.
The training vectors for which 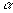 > 0 are
termed the support vectors.
> 0 are
termed the support vectors.
Thus to classify a vector x, we just calculate the sign of
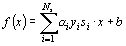 |
(2) |
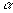 < C and using:
< C and using:
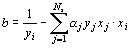
For completeness, the hyperplane is defined as:
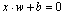
|
(3) |
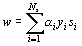
The reason SVMs have been able to perform so well is in the addition of kernel functions to the above algorithm. Kernel functions map the input vectors to some higher dimensioned space such that a more suitable hyperplane can be found with minimal classification errors. The kernel function is defined as
|
|
(4) |
 maps the vector x
to some other Euclidean space.
maps the vector x
to some other Euclidean space.
Since we can replace the dot product
xi∑xj with
K(xi,xj) in the algorithm,
there would never be a need to explicitly define what
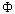 is. Thus the training Lagrangian becomes:
is. Thus the training Lagrangian becomes:
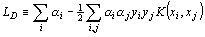
|
(5) |
and the classification function becomes:
|
|
(6) |
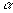 < C and using:
< C and using:
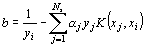
The formulation of kernel functions is only restricted by the
condition that the kernel functions must satisfy the Mercerís
Condition. It states that for a function g(x), where
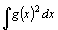 is finite, then
is finite, then 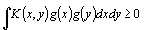 .
.
Table 1 lists some of the common kernel functions.
| Type | Kernel function |
| Polynomial of degree p | 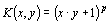 |
| Radial basis function | 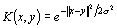 |
| 2-layer sigmoidal neural network | 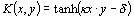 |
Table 1
This provides an overview of SVMs. Burgesí (1998) tutorial gives a more in depth look at them.
References
Burges, CJC "A Tutorial on Support Vector Machines for Pattern Recognition" Data Mining and Knowledge Discovery, Vol 2 No 2, 1998.
Vapnik, V "Estimation of Dependences Based on Empirical Data" [in Russian] Moscow: Nauka, 1997. (English translation: New York: Springer Verlag, 1982)